Gated Recurrent Unit (GRU) Cell Prototype and Function List¶

Description¶

This kernel implements the Gated Recurrent Unit (GRU) cell in version where a reset gate is applied on the hidden state before matrix multiplication (see Depth-Gated Recurrent Neural Networks for more details), as shown in Figure Gated Recurrent Unit Schematic Representation.

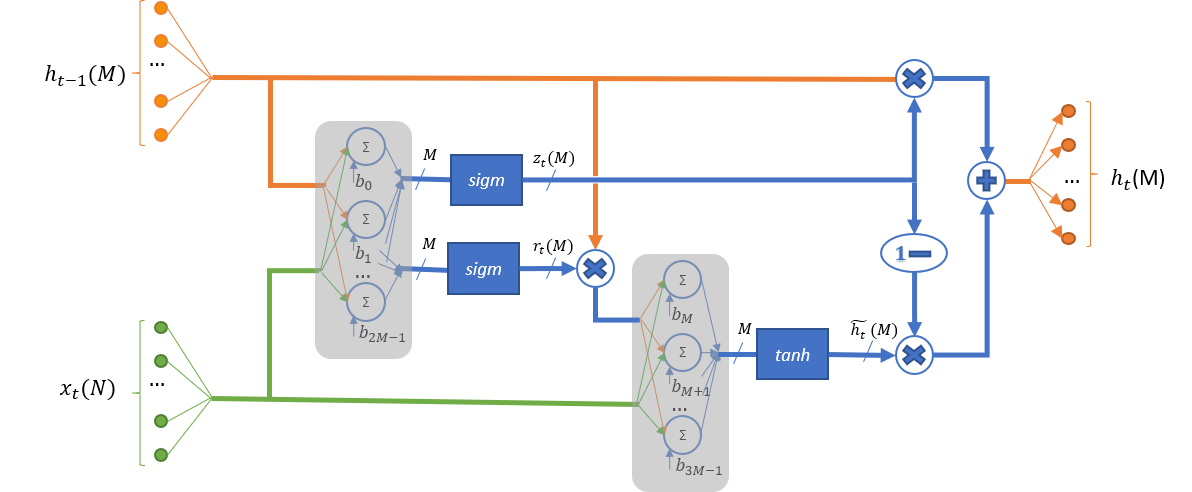
Gated Recurrent Unit Schematic Representation¶

The GRU operation is described by the following formulas:

(1)¶\[ \begin{align}\begin{aligned}{z_{t}} &= {sigm\left( x_{t}W_{\text{xz}} + h_{t - 1}W_{\text{hz}} + b_{z} \right)}\\{r_{t}} &= {sigm\left( x_{t}W_{\text{xr}} + h_{t - 1}W_{\text{hr}} + b_{r} \right)}\\{{\widetilde{h}}_{t}} &= {tanh\left( x_{t}W_{\text{xu}} + (r_{t}*h_{t - 1})W_{\text{hu}} + b_{e} \right)}\\{h_{t}} &= {z_{t}*h_{t - 1} + \left( 1 - z_{t} \right) *{\widetilde{h}}_{t}}\end{aligned}\end{align} \]

Where:

\(\ x_{t}\ \) - frame \(t\) in input sequence.

\(\ h_{t}\ \) - hidden state (also cell output) for frame \(t\) in input sequence.

\(\ {\widetilde{h}}_{t}\ \) - updated hidden state for frame \(t\) in input sequence.

\(z_{t}\ ,\ r_{t}\) - Update and reset gates subtensors for frame \(t\) in input sequence.

\(W_{**}\ \) - weights for appropriate input subtensor.

\(b_{*}\ \) - bias for appropriate input subtensor.

\(sigm\) , \(tanh\) - sigmoid and hyperbolic tangent activation functions.

In the Figure Gated Recurrent Unit Schematic Representation, N is the total number of elements in the input and M is the total number of elements in the cell output.

This kernel uses two look-up tables (LUTs) to perform data transformation. See Look-Up Tables (LUT) Manipulation Prototypes and Function List section and the pseudo-code sample for more details on LUT structure preparation. Use the following functions for the purpose:

mli_krn_tanh_get_lut_size

mli_krn_tanh_create_lut

mli_krn_sigm_get_lut_size

mli_krn_sigm_create_lut

This is a MAC-based kernel which implies accumulation. See Quantization: Influence of Accumulator Bit Depth for more information on related quantization aspects. The number of accumulation series is equal to single input frame size plus single output frame size.

Functions¶

Kernels which implement an GRU cell have the following prototype:

mli_status mli_krn_gru_cell_<data_format>(
   const mli_tensor *in,
   const mli_tensor *prev_out,
   const mli_tensor *weights_in,
   const mli_tensor *weights_out,
   const mli_tensor *bias,
   const mli_lut * tanh_lut,
   const mli_lut * sigm_lut,
   const mli_rnn_cell_cfg *cfg,
   mli_tensor *out);

where data_format is one of the data formats listed in Table MLI Data Formats and the function parameters are shown in the following table:

GRU Cell Function Parameters¶
Parameter	Type	Description
`in`	`mli_tensor *`	[IN] Pointer to constant input tensor.
`prev_out`	`mli_tensor *`	[IN] Pointer to constant previous output tensor.
`weights_in`	`mli_tensor *`	[IN] Pointer to constant weights tensor for GRU input.
`weights_out`	`mli_tensor *`	[IN] Pointer to constant weights tensor for GRU output.
`bias`	`mli_tensor *`	[IN] Pointer to constant bias tensor.
`tanh_lut`	`mli_lut *`	[IN] Pointer to a valid LUT table structure prepared for the hyperbolic tangent activation.
`sigm_lut`	`mli_lut *`	[IN] Pointer to a valid LUT table structure prepared for the sigmoid activation.
`cfg`	`mli_rnn_cell_cfg *`	[IN \| OUT] Pointer to RNN cell parameters structure.
`out`	`mli_tensor *`	[IN \| OUT] Pointer to output tensor. Result is stored here.

Fields of mli_rnn_cell_cfg structure are described in table mli_rnn_cell_cfg Structure Field Description.

Weights for the cell consist of two tensors:

weights_in: a three-dimensional tensor of shape (3, N, M) where N is a number of elements in input tensor, and M is a number of elements in hidden state (equal to number of elements in output tensor). It represents stacking of weights using the GRU operation (1) in order (z, r, u):

\[\begin{split}\begin{bmatrix} W_{\text{xz}} & W_{\text{xr}} & W_{\text{xu}} \\ \end{bmatrix}\end{split}\]

weights_out: a three-dimensional tensor of shape (3, M, M) where M is a number of cell elements (weights which involved into a single dot product series are stored column wise, that is, with M stride in memory). It represents stacking of weights using the GRU operation (1) in order (z, r, u):

\[\begin{split}\begin{bmatrix} W_{\text{hz}} & W_{\text{hr}} & W_{\text{hu}} \\ \end{bmatrix}\end{split}\]

bias tensor of shape (3, M) keeps subtensors in the same order:

\[\begin{split}\begin{bmatrix} b_{z} & b_{r} & b_{u} \\ \end{bmatrix}\end{split}\]

This kernel implies sequential processing of the set of inputs vectors (or timesteps) which is passed by input tensor of shape (sequence_length, N) where N is the length of the single frame \(x_{t}\) . Both directions of processing (forward and backward) are supported and defined by cfg structure. The Kernel can output the bunch of results for according to each step of processing, or only the last one in the sequence.

Dense part of calculations uses scratch data from configuration structure for results, and consequently output and previous output tensors might use the same memory if it is acceptable to rewrite previous output data. Ensure that you allocate memory for the rest of the tensors and for scratch data from cfg structure without overlaps. Otherwise the behavior is undefined.

The following table lists all the available GRU cell functions:

List of Available GRU Cell Functions¶
Function Name	Details
`mli_krn_gru_cell_sa8_sa8_sa32`	In/out/weights data format: sa8 Bias data format: sa32
`mli_krn_gru_cell_fx16`	All tensors data format: fx16
`mli_krn_gru_cell_fx16_fx8_fx8`	In/out data format: fx16 weights/Bias data format: fx8

Conditions¶

Ensure that you satisfy the following general conditions before calling the function:

in, out, prev_out, weights_in, weights_out and bias tensors must be valid (see mli_tensor Structure Field Descriptions) and satisfy data requirements of the selected version of the kernel.

tanh_lut and sigm_lut structures must be valid and prepared for hyperbolic tangent and sigmoid activation functions accordingly (see Look-Up Tables (LUT) Manipulation Prototypes and Function List).

Shapes of in, out, prev_out, weights_in, weights_out and bias tensors must be compatible, which implies the following requirements:

in must be a 2-dimensional tensor (rank==2) of shape (sequence_length, \(N\)) where sequence_length is a number of input frames (or timesteps) for sequential processing by GRU cell.

weights_in must be a 3-dimensional tensor (rank==3) of shape (3, \(N\), \(M\)).

weights_out must be a 3-dimensional tensor (rank==3) of shape (3, \(M\), \(M\)).

bias must be a 2-dimensional tensor (rank==2) of shape (3, \(M\)).

prev_out must be a one-dimensional tensor (rank==1) of shape (\(M\)).

out tensor might be of any shape and rank. Kernel changes its shape to (sequence_length, \(M\))

out.data container must point to a buffer with sufficient capacity for storing the result (to keep \(M\) elements if GRU cell is configured with RNN_OUT_LAST or to keep \(M*sequence\_length\) elements if GRU cell is configured with RNN_OUT_ALL).

scratch_data field in config structure must contain a valid pointer to a buffer with sufficient capacity for the intermediate result (\(3*M\) elements of input type). The capacity field of the scratch_data must reflect the available size of this memory in bytes properly (see Table mli_rnn_cell_cfg Structure Field Description).

in.data and cfg->scratch_data containers must not point to overlapped memory regions.

mem_stride must satisfy the following statements:

For in, prev_out and out tensors - memstride must reflect the shape, e.g memory of these tensors must be contiguous

For weights_in, weights_out and bias tensor - memstride of the innermost dimension must be equal to 1.

For fx16 and fx16_fx8_fx8 versions of kernel, in addition to the general conditions, ensure that you satisfy the following quantization conditions before calling the function:

The number of frac_bits in the bias tensor must not exceed the sum of frac_bits in the in and weights_in tensors.

For sa8_sa8_sa32 versions of kernel, in addition to the general conditions, ensure that you satisfy the following quantization conditions before calling the function:

in, out and prev_out tensor must be quantized on the tensor level. This implies that each tensor contains a single scale factor and a single zero offset.

Zero offset of in, out and prev_out tensors must be within [-128, 127] range.

weights_in, weights_out and bias tensors must be symmetric. All these tensors must be quantized on the same level. Allowed Options:

Per Tensor level. This implies that each tensor contains a single scale factor and a single zero offset equal to 0.

Per First Dimension level (number of sub-tensors equal to 3). This implies that each tensor contains separate scale point for each sub-tensor. All tensors contain single zero offset equal to 0.

Scale factors of bias tensor must be equal to the multiplication of in scale factor broadcasted on weights_in array of scale factors. See the example for the similar condition in the Convolution 2D Prototype and Function List.

Ensure that you satisfy the platform-specific conditions in addition to those listed above (see the Platform Specific Details chapter).

Result¶

These functions modify:

shape, rank and mem_stride of out tensor.

memory pointed by out.data.mem field.

memory pointed by cfg.scratch_data.mem fields.

It is assumed that all the other fields and structures are properly populated to be used in calculations and are not modified by the kernel.

Depending on the debug level (see section Error Codes) this function performs a parameter check and returns the result as an mli_status code as described in section Kernel Specific Configuration Structures.