MLI Kernels (Operators)

This chapter introduces into a general concept of ML algorithms (kernels) included in MLI 2.0.

Each kernel is implemented as a separate function, and inputs and outputs are represented by the tensor structure defined in section mli_tensor Structure. A kernel can have multiple specializations, each implemented as a separate function. As a result, the neural network graph implementation is represented as series of function calls, which can either be constructed manually by the user or via some automated front-end tool.

The following groups of NN kernels are defined:

• Convolution Kernels Group

• Recurrent and Fully Connected Kernels Group

• Pooling Kernels Group

• Diverse Kernels Group

• Transform (Activation) Kernels Group

• Element-wise Kernels Group

Function Names and Specializations

All function names of the kernels are constructed in a similar way. To make it easier to navigate through the list of API functions, all function names are built using the following syntax:

mli_<group>_<function>_[layout_]<dataformats>[_specializations]([input_tensors],[cfg],[output_tensors]);

An explanation of each of the preceding elements which make up a name is provided in Table Function Naming Convention Fields. The function arguments start with zero or more input tensors, followed by a kernel specific configuration struct, followed by the output tensors. All the function parameters are grouped inside the config structure.

Function Naming Convention Fields

Field Name	Examples	Description
Group	krn hlp mov usr	krn for compute kernels hlp for helper functions mov for data move kernels usr for user-defined kernels.
Functions	conv2d fully_connected …	Describes the basic functionality. Full list of supported function names is described later
layout	chw hwcn nhwc	Optional description of the layout of the input, only relevant for some functions
dataformats	fx16 sa8_sa8_sa32 sa8	Specifies the tensor data formats. In case of multiple input tensors with different data formats, the format of each tensor is specified in the same order as the function arguments. (for details see mli_element_params Union Field Description).

The naming convention for the data formats is as follows and in Data Format Naming Convention Fields:

<typename><containersize>

Data Format Naming Convention Fields

Field Name	Examples	Description
typename	fx sa fp	Specifies which quantization schema is used: fx for Fixed point sa for Signed Asymmetric fp for Floating Point
containersize	1, 4, 8, 16, 32	Container size in bits of each individual element.

The following convention is applied to the layout field:

• If MLI kernel implies using only three-dimensional variable tensors as input/output, function name should reflect layout of input and output tensors. Layout of input and output must be the same.

• If MLI kernel implies using four-dimensional weights tensor in addition to three-dimensional input/output tensors, function name should reflect layout of weights tensor.

A Note on Slicing

The kernels described in the following sections of this document have no notion of slicing (also referred to as tiling). Instead, the responsibility of slicing is left to the caller, which can be either application code, some higher-level API or graph-compiler generated. For cores with any sort of closely-coupled memory (CCMs), the kernels assume that all the input tensors are in CCM. The output tensor can be either in system memory or in CCM.

Slicing is required in case there is not enough space in CCM to fit the complete input tensors. In this case, the caller can copy a ‘slice’ of the input tensor into CCM, and the kernel produces a slice of the output tensor. These output slices can be combined into a full tensor. Because the tensor data does not have to be contiguous in memory, it is possible to create a (slice) tensor that points to a subset of the data of a larger tensor. For instance, if the output tensor is in system memory, each invocation of the kernel that computes a slice can write its output directly into the correct (slice) of the output tensor. This eliminates the need for an extra concatenation copy pass. The slicing concept is illustrated in Figure Slicing Concept.

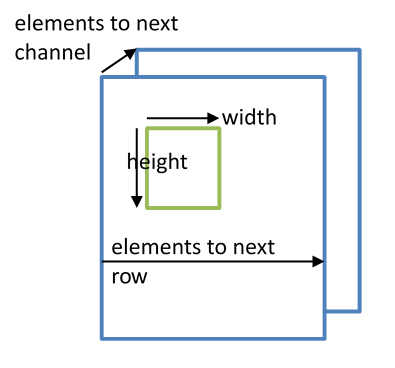
Slicing Concept

If the tensors don’t fit into CCM, and there is no data cache, the data move functions can be used to copy full tensors or slices of tensors. (see Chapter Data Movement ). Slicing with some kernels requires updating the kernel parameters when passing each slice.

The number of elements to the next dimension is stored in the mem_stride field (as described in mli_tensor Structure Field Descriptions). In case there is no slicing or concatenation, the mem_stride field is populated in alignement with the shape values to reflect the offsets in the data buffers for each dimension.