Convolution 2D Prototype and Function List¶

Description¶

This kernel implements a general 2D convolution operation. It applies each filter of weights tensor to each framed area of the size of input tensor.

The convolution operation is shown in Figure Convolution 2D.

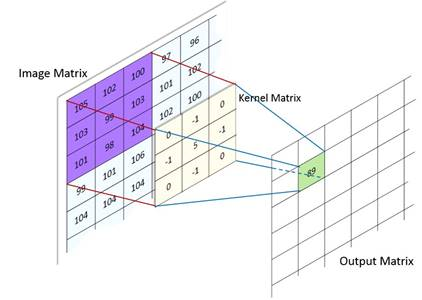
Convolution 2D¶

For example, in a HWCN data layout, if the in feature map is \((Hi, Wi, Ci)\) and the weights is \((Hk, Wk, Ci, Co)\), the output feature map is \((Ho, Wo, Co)\) tensor where the spatial dimensions comply with the system of equations (1).

Note

For more details on calculations, see chapter 2 of A guide to convolution arithmetic for deep learning.

Optionally, saturating ReLU activation function can be applied to the result of the convolution during the function’s execution. For more information on supported ReLU types and calculations, see ReLU Prototype and Function List.

This is a MAC-based kernel which implies accumulation. See Quantization: Influence of Accumulator Bit Depth for more information on related quantization aspects. The Number of accumulation series in terms of above-defined variables is equal to \((Hk * Wk * Ci)\).

Functions¶

The functions which implement 2D Convolutions have the following prototype:

mli_status mli_krn_conv2d_hwcn_<data_format>(
  const mli_tensor *in,
  const mli_tensor *weights,
  const mli_tensor *bias,
  const mli_conv2d_cfg *cfg,
  mli_tensor *out);

where data_format is one of the data formats listed in Table MLI Data Formats and the function parameters are shown in the following table:

2D Convolution Function Parameters¶
Parameter	Type	Description
`in`	`mli_tensor *`	[IN] Pointer to constant input tensor
`weights`	`mli_tensor *`	[IN] Pointer to constant weights tensor
`bias`	`mli_tensor *`	[IN] Pointer to constant bias tensor
`cfg`	`mli_conv2d_cfg *`	[IN] Pointer to convolution parameters structure
`out`	`mli_tensor *`	[IN \| OUT] Pointer to output feature map tensor. Result is stored here

Here is a list of all available 2D Convolution functions:

List of Available 2D Convolution Functions¶
Function Name	Details
`mli_krn_conv2d_hwcn_sa8_sa8_sa32`	In/out layout: HWC Weights layout: HWCN In/out/weights data format: sa8 Bias data format: sa32
`mli_krn_conv2d_hwcn_fx16`	In/out layout: HWC Weights layout: HWCN All tensors data format: fx16
`mli_krn_conv2d_hwcn_fx16_fx8_fx8`	In/out layout: HWC Weights layout: HWCN In/out data format: fx16 Weights/Bias data format: fx8
`mli_krn_conv2d_hwcn_sa8_sa8_sa32_k1x1`	In/out layout: HWC Weights layout: HWCN In/out/weights data format: sa8 Bias data format: sa32 Width of weights tensor: 1 Height of weights tensor: 1
`mli_krn_conv2d_hwcn_fx16_k1x1`	In/out layout: HWC Weights layout: HWCN All tensors data format: fx16 Width of weights tensor: 1 Height of weights tensor: 1
`mli_krn_conv2d_hwcn_fx16_fx8_fx8_k1x1`	In/out layout: HWC Weights layout: HWCN In/out data format: fx16 Weights/Bias data format: fx8 Width of weights tensor: 1 Height of weights tensor: 1
`mli_krn_conv2d_hwcn_sa8_sa8_sa32_k3x3`	In/out layout: HWC Weights layout: HWCN In/out/weights data format: sa8 Bias data format: sa32 Width of weights tensor: 3 Height of weights tensor: 3
`mli_krn_conv2d_hwcn_fx16_k3x3`	In/out layout: HWC Weights layout: HWCN All tensors data format: fx16 Width of weights tensor: 3 Height of weights tensor: 3
`mli_krn_conv2d_hwcn_fx16_fx8_fx8_k3x3`	In/out layout: HWC Weights layout: HWCN In/out data format: fx16 Weights/Bias data format: fx8 Width of weights tensor: 3 Height of weights tensor: 3
`mli_krn_conv2d_hwcn_sa8_sa8_sa32_k5x5`	In/out layout: HWC Weights layout: HWCN In/out/weights data format: sa8 Bias data format: sa32 Width of weights tensor: 5 Height of weights tensor: 5
`mli_krn_conv2d_hwcn_fx16_k5x5`	In/out layout: HWC Weights layout: HWCN All tensors data format: fx16 Width of weights tensor: 5 Height of weights tensor: 5
`mli_krn_conv2d_hwcn_fx16_fx8_fx8_k5x5`	In/out layout: HWC Weights layout: HWCN In/out data format: fx16 Weights/Bias data format: fx8 Width of weights tensor: 5 Height of weights tensor: 5

Conditions¶

Ensure that you satisfy the following general conditions before calling the function:

in, out, weights and bias tensors must be valid (see mli_tensor Structure Field Descriptions) and satisfy data requirements of the selected version of the kernel.

Shapes of in, out, weights and bias tensors must be compatible, which implies the following requirements:

in and out are 3-dimensional tensors (rank==3). Dimensions meaning, and order (layout) is aligned with the specific version of kernel.

weights is a 4-dimensional tensor (rank==4). Dimensions meaning, and order (layout) is aligned with the specific kernel.

bias must be a one-dimensional tensor (rank==1). Its length must be equal to \(Co\) (output channels OR number of filters).

Channel \(Ci\) dimension of in and weights tensors must be equal.

Shapes of in, out and weights tensors together with cfg structure must satisfy the equations (1)

Effective width and height of the weights tensor after applying dilation factor (see (1)) must not exceed appropriate dimensions of the in tensor.

in and out tensors must not point to overlapped memory regions.

mem_stride of the innermost dimension must be equal to 1 for all the tensors.

padding_top and padding_bottom parameters must be in the range of [0, \(\hat{Hk}\)) where \(\hat{Hk}\) is the effective kernel height (See (1))

padding_left and padding_right parameters must be in the range of [0, \(\hat{Wk}\)) where \(\hat{Wk}\) is the effective kernel width (See (1))

stride_width and stride_height parameters must not be equal to 0.

dilation_width and dilation_height parameters must not be equal to 0.

For fx16 and fx16_fx8_fx8 versions of kernel, in addition to the general conditions, ensure that you satisfy the following quantization conditions before calling the function:

The number of frac_bits in the bias and out tensors must not exceed the sum of frac_bits in the in and weights tensors.

For sa8_sa8_sa32 versions of kernel, in addition to general conditions, ensure that you satisfy the following quantization conditions before calling the function:

in and out tensors must be quantized on the tensor level. This implies that each tensor contains a single scale factor and a single zero offset.

Zero offset of in and out tensors must be within [-128, 127] range.

weights and bias tensors must be symmetric. Both must be quantized on the same level. Allowed Options:

Per tensor level. This implies that each tensor contains a single scale factor and a single zero offset equal to 0.

Per \(Co\) dimension level (number of filters). This implies that each tensor contains separate scale point for each sub-tensor. All tensors contain single zero offset equal to 0.

Scale factors of bias tensor must be equal to the multiplication of input scale factor broadcasted on weights array of scale factors.

Example

Having source float scales for input and weights operands, bias sclale in C code can be calculated in the following way with help of standart frexpf function:

// Bias scale must be equal to the multiplication of input
// and weights scales
const float in_scale = 0.00392157f;
const float w_scale_1 = 0.00542382f;
float bias_scale = in_w_scale * w_scale_1;

// Derive quantized bias scale and frac bits for use in tensor struct.
int exp;
frexpf(bias_scale, &exp);
int bias_scale_frac_bits = 15 - exp;
int16_t bias_scale_val = (int16_t)((1ll << frac_bits) * bias_scale + 0.5f);

Ensure that you satisfy the platform-specific conditions in addition to those listed above (see the Platform Specific Details chapter).

Result¶

These functions only modify the memory pointed by out.data.mem field. It is assumed that all the other fields of out tensor are properly populated to be used in calculations and are not modified by the kernel.

Depending on the debug level (see section Error Codes) these functions might perform a parameter check and return the result as an mli_status code as described in section Kernel Specific Configuration Structures.